Extracting the V matrix for MLMs
Notes to self (and anyone else who might find this useful). With the general linear mixed models (to simplify, I am just omitting super/subscripts):
where we assume and . is:
Software estimates iteratively and maximizes the likelihood (the function of which depends on whether ML or REML is used). The value of can be obtained using:
.
I just wanted to figure out how to extract from the R output.
1. Manual method
Just using the sleepstudy dataset:
library(lme4)
data(sleepstudy)
nrow(sleepstudy) #total number of observations
[1] 180
dplyr::n_distinct(sleepstudy$Subject) #number of clusters
[1] 18
m1 <- lmer(Reaction ~ Days + (Days | Subject), sleepstudy)
summary(m1)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: Reaction ~ Days + (Days | Subject)
Data: sleepstudy
REML criterion at convergence: 1744
Scaled residuals:
Min 1Q Median 3Q Max
-3.954 -0.463 0.023 0.463 5.179
Random effects:
Groups Name Variance Std.Dev. Corr
Subject (Intercept) 612.1 24.74
Days 35.1 5.92 0.07
Residual 654.9 25.59
Number of obs: 180, groups: Subject, 18
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 251.41 6.82 17.00 36.84 < 2e-16 ***
Days 10.47 1.55 17.00 6.77 3.3e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr)
Days -0.138
To obtain the matrix:
Z <- getME(m1, 'Z') #180 x 36
G <- bdiag(VarCorr(m1)) #2 x 2
G #the vcov matrix for RE
## 2 x 2 sparse Matrix of class "dsCMatrix"
## (Intercept) Days
## (Intercept) 612.1 9.6
## Days 9.6 35.1
R <- diag(sigma(m1)^2, nobs(m1)) #180 x 180
is a 2 2 matrix. Need to expand this based on the number of cluster/subjects.
Gm <- kronecker(diag(18), G)
Gm[1:6, 1:6] #just to show this
## 6 x 6 sparse Matrix of class "dgCMatrix"
##
## [1,] 612.1 9.6 . . . .
## [2,] 9.6 35.1 . . . .
## [3,] . . 612.1 9.6 . .
## [4,] . . 9.6 35.1 . .
## [5,] . . . . 612.1 9.6
## [6,] . . . . 9.6 35.1
V <- Z %*% Gm %*% t(Z) + R
Knowing , we can put this together to get the fixed effects:
X <- model.matrix(m1)
y <- m1@resp$y
I will just make a function to put this together:
getFE <- function(X, V, y){
solve(t(X) %*% solve(V) %*% X) %*% t(X) %*% solve(V) %*% y
}
getFE(X, V, y)
## 2 x 1 Matrix of class "dgeMatrix"
## [,1]
## (Intercept) 251.4
## Days 10.5
fixef(m1) #the same
## (Intercept) Days
## 251.4 10.5
Doing this way is fine for simple, well arranged (sorted) datasets but can get more complicated with more levels of clustering (three or more levels). I had to create the Gm matrix.
2. More automated way:
After some Googling, I found this which shows how to make a more general function to construct that matrix. I just put this into a function which will make it easier to call and should work with more complicated RE specifications:
getV <- function(x){
var.d <- crossprod(getME(x, "Lambdat"))
Zt <- getME(x, "Zt")
vr <- sigma(x)^2
var.b <- vr * (t(Zt) %*% var.d %*% Zt)
sI <- vr * Matrix::Diagonal(nobs(x)) #for a sparse matrix
var.y <- var.b + sI
}
Just using the earlier example:
getFE(X, getV(m1), y) #works
## 2 x 1 Matrix of class "dgeMatrix"
## [,1]
## (Intercept) 251.4
## Days 10.5
3. Try it with simple three level data…
Just make a small dataset that is manageable (always helpful to be able to see the data). Five students with 3 teachers in 10 sch (or 15 students per school)
n1 <- 5; n2 = 3; n3 = 10
sch <- letters[1:10] #schoolid
tch <- 1:30 #teacherid
sch.cl <- rep(sch, each = n1 * n2) #cluster var
tch.cl <- rep(tch, each = n1)
set.seed(123)
e3 <- rep(rnorm(n1), each = n1 * n2)
e2 <- rep(rnorm(n2 * n1), each = n1)
x1 <- rnorm(n1 * n2 * n3)
e1 <- rnorm(n1 * n2 * n3)
y <- e3 + e2 + .5 * x1 + e1
dat <- data.frame(y, sch.cl, tch.cl, e3, e2, x1, e1)
dat[1:30, ]
y sch.cl tch.cl e3 e2 x1 e1
1 0.405 a 1 -0.56 1.715 -1.0678 -0.2154
2 1.111 a 1 -0.56 1.715 -0.2180 0.0653
3 0.608 a 1 -0.56 1.715 -1.0260 -0.0341
4 2.919 a 1 -0.56 1.715 -0.7289 2.1285
5 0.101 a 1 -0.56 1.715 -0.6250 -0.7413
6 -2.039 a 2 -0.56 0.461 -1.6867 -1.0960
7 0.357 a 2 -0.56 0.461 0.8378 0.0378
8 0.288 a 2 -0.56 0.461 0.1534 0.3105
9 -0.232 a 2 -0.56 0.461 -1.1381 0.4365
10 0.069 a 2 -0.56 0.461 1.2538 -0.4584
11 -2.676 a 3 -0.56 -1.265 0.4265 -1.0633
12 -0.710 a 3 -0.56 -1.265 -0.2951 1.2632
13 -1.728 a 3 -0.56 -1.265 0.8951 -0.3497
14 -2.252 a 3 -0.56 -1.265 0.8781 -0.8655
15 -1.651 a 3 -0.56 -1.265 0.8216 -0.2363
16 -0.770 b 4 -0.23 -0.687 0.6886 -0.1972
17 0.470 b 4 -0.23 -0.687 0.5539 1.1099
18 -0.863 b 4 -0.23 -0.687 -0.0619 0.0847
19 -0.316 b 4 -0.23 -0.687 -0.3060 0.7541
20 -1.607 b 4 -0.23 -0.687 -0.3805 -0.4993
21 -0.809 b 5 -0.23 -0.446 -0.6947 0.2144
22 -1.104 b 5 -0.23 -0.446 -0.2079 -0.3247
23 -1.214 b 5 -0.23 -0.446 -1.2654 0.0946
24 -0.487 b 5 -0.23 -0.446 2.1690 -0.8954
25 -1.383 b 5 -0.23 -0.446 1.2080 -1.3108
26 2.430 b 6 -0.23 1.224 -1.1231 1.9972
27 1.393 b 6 -0.23 1.224 -0.4029 0.6007
28 -0.491 b 6 -0.23 1.224 -0.4667 -1.2513
29 0.773 b 6 -0.23 1.224 0.7800 -0.6112
30 -0.233 b 6 -0.23 1.224 -0.0834 -1.1855
m2 <- lmer(y ~ x1 + (1|sch.cl/tch.cl), data = dat)
summary(m2)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: y ~ x1 + (1 | sch.cl/tch.cl)
Data: dat
REML criterion at convergence: 490
Scaled residuals:
Min 1Q Median 3Q Max
-2.5495 -0.5604 -0.0782 0.5296 2.0960
Random effects:
Groups Name Variance Std.Dev.
tch.cl:sch.cl (Intercept) 1.226 1.107
sch.cl (Intercept) 0.420 0.648
Residual 0.981 0.991
Number of obs: 150, groups: tch.cl:sch.cl, 30; sch.cl, 10
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 0.3759 0.2991 8.9956 1.26 0.24045
x1 0.3588 0.0922 124.7229 3.89 0.00016 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr)
x1 0.005
Z <- getME(m2, "Z") #n x (sch + tch; just intercepts)
dim(Z)
[1] 150 40
image(Z[1:30,]) #just showing the Z matrix for the first 30 obs
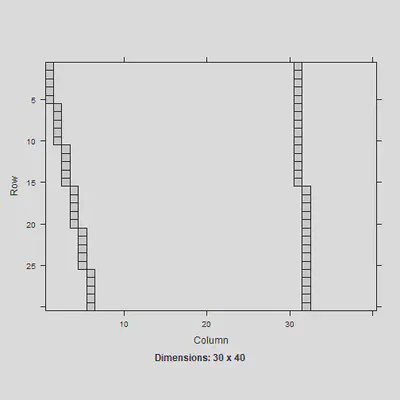
The design matrix is different now since there are more than two levels. This needs to be multiplied by the matrix to follow:
G <- bdiag(VarCorr(m2))
G #how should G then be formed for the Gm?
2 x 2 sparse Matrix of class "dsCMatrix"
[1,] 1.23 .
[2,] . 0.42
Intercept variance on upper left is for teachers and lower right is for schools. Constructing the matrix is relatively straightforward. Doing this manually.
a1 <- kronecker(diag(30), 1.226473) #for teachers
a2 <- kronecker(diag(10), .4201496) #for schools
Gm <- bdiag(a1, a2) #stacking as a diagonal matrix
dim(Gm)
## [1] 40 40
image(Gm)
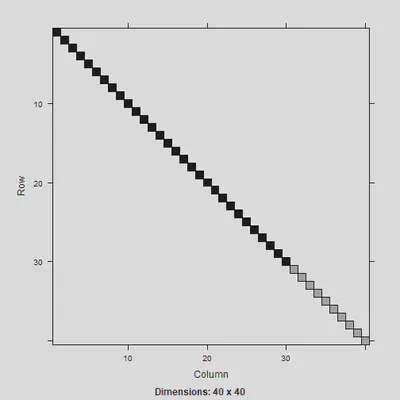
Can then use this to create the matrix:
V <- Z %*% Gm %*% t(Z) + diag(sigma(m2)^2, nobs(m2))
X <- model.matrix(m2)
y <- m2@resp$y
getFE(X, V, y) #compute our fixed effects
## 2 x 1 Matrix of class "dgeMatrix"
## [,1]
## (Intercept) 0.376
## x1 0.359
fixef(m2) #the same
## (Intercept) x1
## 0.376 0.359
If we use our getV function, this just works too which much less hassle!
getFE(X, getV(m2), y)
## 2 x 1 Matrix of class "dgeMatrix"
## [,1]
## (Intercept) 0.376
## x1 0.359
4. Throw in random slopes
The above will only work if the structure of and are simple. If data are not sorted, that may not work.
library(mlmRev)
library(dplyr)
data(star)
set.seed(123)
konly <- filter(star, gr == 'K') %>% sample_frac(.2) #just selecting a few
#so the Z matrix can be seen
m3 <- lmer(read ~ cltype + sx + (sx|sch/tch), data = konly)
X <- model.matrix(m3)
y <- m3@resp$y
Vm <- getV(m3)
getFE(X, Vm, y)
4 x 1 Matrix of class "dgeMatrix"
[,1]
(Intercept) 438.91
cltypereg -5.92
cltypereg+A -2.21
sxF 2.05
fixef(m3) #the same!
(Intercept) cltypereg cltypereg+A sxF
438.91 -5.92 -2.21 2.05
Look at the matrix:
bdiag(VarCorr(m3))
## 4 x 4 sparse Matrix of class "dsCMatrix"
##
## [1,] 141.8 -10.118 . .
## [2,] -10.1 0.722 . .
## [3,] . . 153.9 -6.399
## [4,] . . -6.4 0.266
The Z matrix is a mess!
Z <- getME(m3, 'Z')
image(Z)
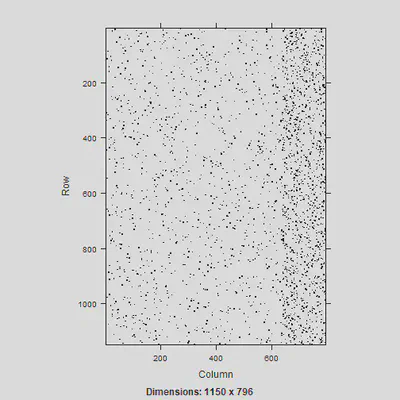
You can compute the matrix per cluster but in this example, just wanted to get the overall matrix.
–END