A while back, I wrote a note about how to conduct a multilevel confirmatory factor analysis (MLCFA) in R. Part of the note shows how to setup lavaan to be able to run the MLCFA model. NOTE: one of the important aspects of an MLCFA is that the factor structure at the two levels may not be the same– that is the factor structures are invariant across levels. The setup process is/was cumbersome– but putting the note together was informative. Testing a 2-1 factor model (i.e., 2 factors at the first level and 1 factor at the second level) required the following code (see the original note for the detailed explanation of the setup and what the variables represent). [This is a measure of school engagement; n = 3,894 students in 254 schools].
1. Running an MLCFA manually
- Read in the data
library(lavaan)## Warning: package 'lavaan' was built under R version 3.4.4## This is lavaan 0.6-3## lavaan is BETA software! Please report any bugs.source('http://faculty.missouri.edu/huangf/data/mcfa/mcfa.R')
raw <- read.csv("http://faculty.missouri.edu/huangf/data/mcfa/raw.csv")
head(raw)## x1 x2 x3 x4 x5 x6 sid
## 1 4 4 3 4 4 3 55
## 2 6 6 4 6 4 4 55
## 3 5 5 2 6 4 4 55
## 4 4 4 5 5 3 3 55
## 5 4 4 4 4 3 2 55
## 6 4 4 2 4 2 2 55Just as a reminder, here are some item statistics:

- Prepare the data for use with the
mcfa.inputfunction to create the necessary matrices and store them inx.
x <- mcfa.input("sid", raw) #sid is the school id or clustering variable
combined.cov <- list(within = x$pw.cov, between = x$b.cov)
combined.n <- list(within = x$n - x$G, between = x$G)
x$icc #view intraclass correlation (ICCs) of the six variables## x1 x2 x3 x4 x5 x6
## 0.199 0.247 0.145 0.108 0.248 0.125- Specify the model:
level2.1factor <- '
f1 =~ x1 + c(a,a)*x2 + c(b,b)*x4
f2 =~ x3 + c(c,c)*x5 + c(d,d)*x6
x1 ~~ c(e,e)*x1
x2 ~~ c(f,f)*x2
x3 ~~ c(g,g)*x3
x4 ~~ c(h,h)*x4
x5 ~~ c(i,i)*x5
x6 ~~ c(j,j)*x6
f1 ~~ c(k,k)*f1
f2 ~~ c(l,l)*f2
f1 ~~ c(m,m)*f2
x1b =~ c(0,3.91)*x1
x1b ~~ c(0,NA)*x1b
x2b =~ c(0,3.91)*x2
x2b ~~ c(0,NA)*x2b
x3b =~ c(0,3.91)*x3
x3b ~~ c(0,NA)*x3b
x4b =~ c(0,3.91)*x4
x4b ~~ c(0,NA)*x4b
x5b =~ c(0,3.91)*x5
x5b ~~ c(0,NA)*x5b
x6b =~ c(0,3.91)*x6
x6b ~~ c(0,NA)*x6b
bf1 =~ c(0,1)*x1b + c(0,NA)*x2b + c(0,NA)*x3b + c(0,NA)*x4b +
c(0,NA)*x5b + c(0,NA)*x6b
bf1 ~~ c(0,NA)*bf1 + c(0,0)*f1 + c(0,0)*f2
'The specified model looks like:
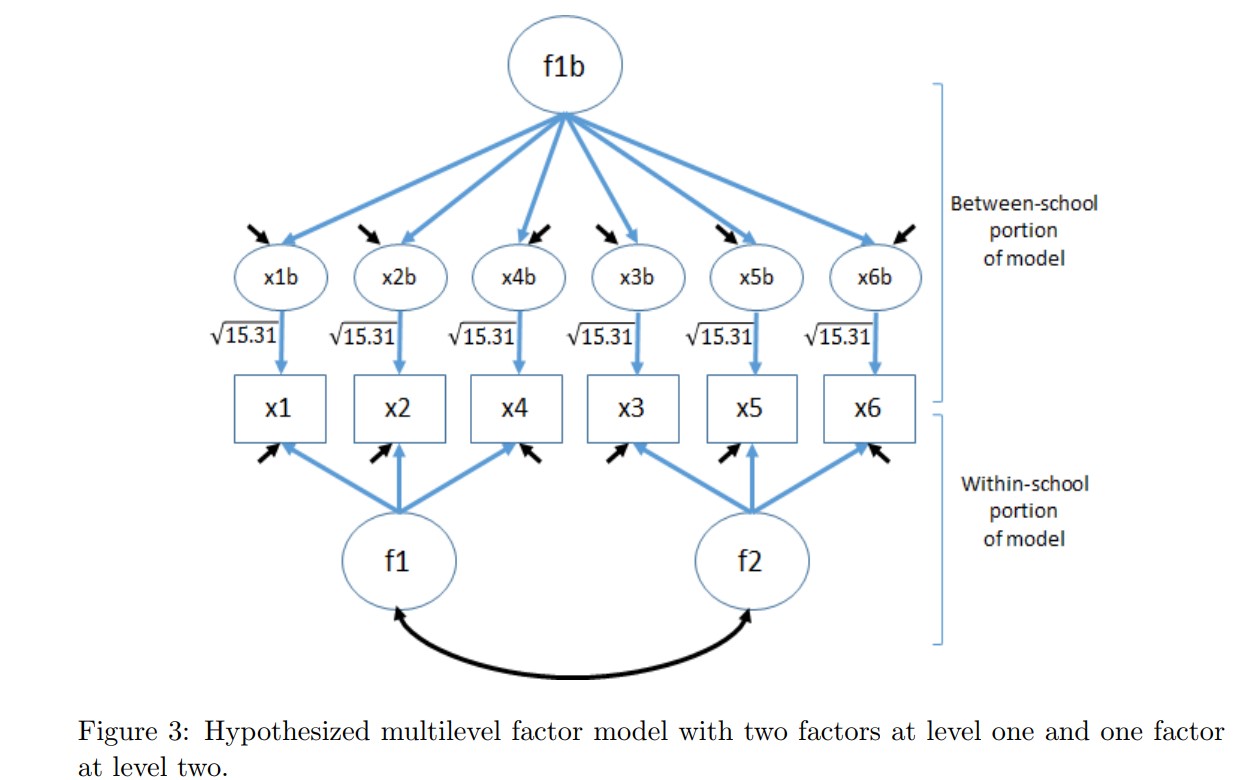
- Run the model:
results6 <- cfa(level2.1factor, sample.cov = combined.cov,
sample.nobs = combined.n, orthogonal = T)
summary(results6, fit.measures = T, standardized = T)## lavaan 0.6-3 ended normally after 54 iterations
##
## Optimization method NLMINB
## Number of free parameters 38
## Number of equality constraints 13
##
## Number of observations per group
## within 3640
## between 254
##
## Estimator ML
## Model Fit Test Statistic 142.465
## Degrees of freedom 17
## P-value (Chi-square) 0.000
##
## Chi-square for each group:
##
## within 56.924
## between 85.541
##
## Model test baseline model:
##
## Minimum Function Test Statistic 11054.075
## Degrees of freedom 30
## P-value 0.000
##
## User model versus baseline model:
##
## Comparative Fit Index (CFI) 0.989
## Tucker-Lewis Index (TLI) 0.980
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -27509.959
## Loglikelihood unrestricted model (H1) -27438.727
##
## Number of free parameters 25
## Akaike (AIC) 55069.919
## Bayesian (BIC) 55226.599
## Sample-size adjusted Bayesian (BIC) 55147.160
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.062
## 90 Percent Confidence Interval 0.052 0.071
## P-value RMSEA <= 0.05 0.019
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.024
##
## Parameter Estimates:
##
## Information Expected
## Information saturated (h1) model Structured
## Standard Errors Standard
##
##
## Group 1 [within]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## f1 =~
## x1 1.000 0.694 0.882
## x2 (a) 1.081 0.021 51.609 0.000 0.750 0.873
## x4 (b) 0.649 0.024 27.156 0.000 0.450 0.454
## f2 =~
## x3 1.000 0.688 0.634
## x5 (c) 1.146 0.030 38.404 0.000 0.789 0.819
## x6 (d) 1.317 0.034 38.786 0.000 0.906 0.868
## x1b =~
## x1 0.000 0.000 0.000
## x2b =~
## x2 0.000 0.000 0.000
## x3b =~
## x3 0.000 0.000 0.000
## x4b =~
## x4 0.000 0.000 0.000
## x5b =~
## x5 0.000 0.000 0.000
## x6b =~
## x6 0.000 0.000 0.000
## bf1 =~
## x1b 0.000 NaN NaN
## x2b 0.000 NaN NaN
## x3b 0.000 NaN NaN
## x4b 0.000 NaN NaN
## x5b 0.000 NaN NaN
## x6b 0.000 NaN NaN
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## f1 ~~
## f2 (m) 0.301 0.013 24.014 0.000 0.630 0.630
## bf1 0.000 NaN NaN
## f2 ~~
## bf1 0.000 NaN NaN
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .x1 (e) 0.137 0.008 17.000 0.000 0.137 0.222
## .x2 (f) 0.176 0.010 18.328 0.000 0.176 0.238
## .x3 (g) 0.704 0.019 37.860 0.000 0.704 0.598
## .x4 (h) 0.781 0.019 41.160 0.000 0.781 0.794
## .x5 (i) 0.306 0.012 25.779 0.000 0.306 0.330
## .x6 (j) 0.270 0.014 19.493 0.000 0.270 0.247
## f1 (k) 0.481 0.016 30.196 0.000 1.000 1.000
## f2 (l) 0.473 0.024 20.059 0.000 1.000 1.000
## x1b 0.000 NaN NaN
## x2b 0.000 NaN NaN
## x3b 0.000 NaN NaN
## x4b 0.000 NaN NaN
## x5b 0.000 NaN NaN
## x6b 0.000 NaN NaN
## bf1 0.000 NaN NaN
##
##
## Group 2 [between]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## f1 =~
## x1 1.000 0.694 0.407
## x2 (a) 1.081 0.021 51.609 0.000 0.750 0.360
## x4 (b) 0.649 0.024 27.156 0.000 0.450 0.270
## f2 =~
## x3 1.000 0.688 0.343
## x5 (c) 1.146 0.030 38.404 0.000 0.789 0.345
## x6 (d) 1.317 0.034 38.786 0.000 0.906 0.496
## x1b =~
## x1 3.910 1.511 0.887
## x2b =~
## x2 3.910 1.900 0.911
## x3b =~
## x3 3.910 1.685 0.841
## x4b =~
## x4 3.910 1.341 0.804
## x5b =~
## x5 3.910 2.073 0.907
## x6b =~
## x6 3.910 1.497 0.820
## bf1 =~
## x1b 1.000 0.987 0.987
## x2b 1.258 0.037 33.807 0.000 0.987 0.987
## x3b 1.025 0.062 16.612 0.000 0.906 0.906
## x4b 0.784 0.054 14.640 0.000 0.871 0.871
## x5b 1.256 0.064 19.471 0.000 0.903 0.903
## x6b 0.991 0.047 21.132 0.000 0.986 0.986
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## f1 ~~
## f2 (m) 0.301 0.013 24.014 0.000 0.630 0.630
## bf1 0.000 0.000 0.000
## f2 ~~
## bf1 0.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .x1 (e) 0.137 0.008 17.000 0.000 0.137 0.047
## .x2 (f) 0.176 0.010 18.328 0.000 0.176 0.040
## .x3 (g) 0.704 0.019 37.860 0.000 0.704 0.175
## .x4 (h) 0.781 0.019 41.160 0.000 0.781 0.281
## .x5 (i) 0.306 0.012 25.779 0.000 0.306 0.058
## .x6 (j) 0.270 0.014 19.493 0.000 0.270 0.081
## f1 (k) 0.481 0.016 30.196 0.000 1.000 1.000
## f2 (l) 0.473 0.024 20.059 0.000 1.000 1.000
## x1b 0.004 0.002 1.742 0.082 0.027 0.027
## x2b 0.006 0.003 1.812 0.070 0.025 0.025
## x3b 0.033 0.008 4.161 0.000 0.179 0.179
## x4b 0.028 0.007 3.814 0.000 0.241 0.241
## x5b 0.052 0.008 6.639 0.000 0.185 0.185
## x6b 0.004 0.004 0.985 0.325 0.027 0.027
## bf1 0.145 0.017 8.637 0.000 1.000 1.0002. Automatic Setup of an MLCFA
To run this automatically using lavaan, the setup is now much simpler:
twolevel <- '
level: 1
f1 =~ x1 + x2 + x4
f2 =~ x3 + x5 + x6
level: 2
fb =~ x1 + x2 + x3 + x4 + x5 + x6
'
results <- cfa(twolevel, data = raw, cluster = 'sid')
summary(results, fit.measures = T, standardized = T)## lavaan 0.6-3 ended normally after 73 iterations
##
## Optimization method NLMINB
## Number of free parameters 31
##
## Number of observations 3894
## Number of clusters [sid] 254
##
## Estimator ML
## Model Fit Test Statistic 140.120
## Degrees of freedom 17
## P-value (Chi-square) 0.000
##
## Model test baseline model:
##
## Minimum Function Test Statistic 10848.717
## Degrees of freedom 30
## P-value 0.000
##
## User model versus baseline model:
##
## Comparative Fit Index (CFI) 0.989
## Tucker-Lewis Index (TLI) 0.980
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -27492.948
## Loglikelihood unrestricted model (H1) -27422.888
##
## Number of free parameters 31
## Akaike (AIC) 55047.896
## Bayesian (BIC) 55242.179
## Sample-size adjusted Bayesian (BIC) 55143.675
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.043
## 90 Percent Confidence Interval 0.037 0.050
## P-value RMSEA <= 0.05 0.953
##
## Standardized Root Mean Square Residual (corr metric):
##
## SRMR (within covariance matrix) 0.022
## SRMR (between covariance matrix) 0.055
##
## Parameter Estimates:
##
## Information Observed
## Observed information based on Hessian
## Standard Errors Standard
##
##
## Level 1 [within]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## f1 =~
## x1 1.000 0.693 0.881
## x2 1.084 0.021 52.810 0.000 0.751 0.874
## x4 0.644 0.024 27.003 0.000 0.446 0.449
## f2 =~
## x3 1.000 0.688 0.634
## x5 1.146 0.030 38.464 0.000 0.789 0.819
## x6 1.321 0.034 38.847 0.000 0.908 0.869
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## f1 ~~
## f2 0.301 0.012 24.171 0.000 0.631 0.631
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .x1 0.000 0.000 0.000
## .x2 0.000 0.000 0.000
## .x4 0.000 0.000 0.000
## .x3 0.000 0.000 0.000
## .x5 0.000 0.000 0.000
## .x6 0.000 0.000 0.000
## f1 0.000 0.000 0.000
## f2 0.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .x1 0.138 0.008 17.530 0.000 0.138 0.223
## .x2 0.175 0.009 18.669 0.000 0.175 0.237
## .x4 0.790 0.019 41.008 0.000 0.790 0.799
## .x3 0.705 0.019 38.015 0.000 0.705 0.598
## .x5 0.306 0.012 25.811 0.000 0.306 0.329
## .x6 0.269 0.014 19.432 0.000 0.269 0.246
## f1 0.481 0.016 30.197 0.000 1.000 1.000
## f2 0.473 0.024 19.969 0.000 1.000 1.000
##
##
## Level 2 [sid]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## fb =~
## x1 1.000 0.385 0.988
## x2 1.262 0.037 34.133 0.000 0.486 0.986
## x3 0.997 0.067 14.861 0.000 0.384 0.899
## x4 0.790 0.054 14.611 0.000 0.304 0.911
## x5 1.209 0.071 17.078 0.000 0.466 0.898
## x6 0.987 0.050 19.704 0.000 0.380 0.988
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .x1 4.744 0.028 168.611 0.000 4.744 12.167
## .x2 4.564 0.035 131.910 0.000 4.564 9.253
## .x3 3.513 0.033 107.212 0.000 3.513 8.225
## .x4 4.348 0.027 160.857 0.000 4.348 13.024
## .x5 4.198 0.037 114.219 0.000 4.198 8.095
## .x6 3.913 0.030 130.439 0.000 3.913 10.168
## fb 0.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .x1 0.004 0.002 1.824 0.068 0.004 0.024
## .x2 0.007 0.003 2.271 0.023 0.007 0.028
## .x3 0.035 0.008 4.100 0.000 0.035 0.191
## .x4 0.019 0.008 2.495 0.013 0.019 0.170
## .x5 0.052 0.008 6.554 0.000 0.052 0.193
## .x6 0.003 0.004 0.946 0.344 0.003 0.023
## fb 0.148 0.018 8.274 0.000 1.000 1.000The factor loadings and fit indices are similar– and are exactly the same when done using Mplus (see article p. 15 for a comparison).
To get the alpha at either level (part of the function), can use the alpha function (I prefer Omega nowadays though for several reasons).
alpha(x$ab.cov) #multilevel alpha or level 2 alpha## [1] 0.9658581NOTE: At the moment, you cannot use ordinal data in a two level model using lavaan and WLSMV.
- END ###