Centering often reduces the correlation between the individual variables (x1, x2) and the product term (x1 \(\times\) x2). In the example below, r(x1, x1x2) = .80. With the centered variables, r(x1c, x1x2c) = -.15.
NOTE: For examples of when centering may not reduce multicollinearity but may make it worse, see EPM article.
set.seed(123)
x1 <- rnorm(100, 10, 1)
x2 <- rnorm(100, 15, 1)
x1x2 <- x1*x2
x1c <- x1 - mean(x1)
x2c <- x2 - mean(x2)
x1x2c <- x1c * x2c
dat <- data.frame(x1, x2, x1x2, x1c, x2c, x1x2c)
round(cor(dat), 2)## x1 x2 x1x2 x1c x2c x1x2c
## x1 1.00 -0.05 0.80 1.00 -0.05 -0.15
## x2 -0.05 1.00 0.55 -0.05 1.00 -0.17
## x1x2 0.80 0.55 1.00 0.80 0.55 -0.17
## x1c 1.00 -0.05 0.80 1.00 -0.05 -0.15
## x2c -0.05 1.00 0.55 -0.05 1.00 -0.17
## x1x2c -0.15 -0.17 -0.17 -0.15 -0.17 1.00A question though may be raised why centering reduces collinearity?
Consider the basic equation for a correlation:
\[r_{(X, Y)} = \frac{cov(X,Y)}{\sqrt{(var(X) \cdot var(Y))}}\]
For the product score (X1X2) and X1:
\[r_{(X1X2, X1) = \frac{cov(X1X2, X1)}{\sqrt{(var(X1X2) \cdot var(X1))}}}\]
Focusing only on the numerator and using covariance algebra, the covariance of a product score (X1X2) with another variable (X1) can be written as:
\[cov(AB, C) = \mathbb{E}(A) \cdot cov(B, C) + \mathbb{E}(B) \cdot cov(A, C)\] \[= \mathbb{E}(X1) \cdot cov(X2, X1) + \mathbb{E}(X2) \cdot cov(X1, X1)\] \[= \mathbb{E}(X1) \cdot cov(X2, X1) + \mathbb{E}(X2) \cdot var(X1)\]
With mean-centered variables:
\[r_{((X1 - \bar{X}1)(X2 - \bar{X}2), (X1 - \bar{X}1))} = \frac{cov((X1 - \bar{X}1)(X2 - \bar{X}2), (X1 - \bar{X}1))}{\sqrt{var((X1 - \bar{X}1)(X2 - \bar{X}2)) \cdot var((X1 - \bar{X}1))}}\]
Focusing only on the numerator again:
\[= \mathbb{E}(X1 - \bar{X}1) \cdot cov(X2 - \bar{X}2, X1 - \bar{X}1) + \mathbb{E}(X2 - \bar{X}2) \cdot cov(X1 - \bar{X}1, X1 - \bar{X}1)\] \[= \mathbb{E}(X1 - \bar{X}1) \cdot cov(X2 - \bar{X}2, X1 - \bar{X}1) + \mathbb{E}(X2 - \bar{X}2) \cdot var(X1 - \bar{X}1)\]
The expected value though of a mean centered variable is zero. So if the numerator is zero, the whole equation reduces to zero (on average).
\[= 0 \cdot cov(X2 - \bar{X}2, X1 - \bar{X}1) + 0 \cdot var(X1 - \bar{X}1)\]
Using a short simulation
- Randomly generate 100 x1 and x2 variables
- Mean center the variables
- Compute corresponding interactions (x1x2 and x1x2c)
- Get the correlations of the variables and the product term (
ris for the raw variables,cris for the centered variables) - Get the average of the terms over the replications
set.seed(4567)
reps <- 1000
r1 <- r2 <- cr1 <- cr2 <- numeric(reps)
for (i in 1:reps){
x1 <- rnorm(100, 10, 1) #mean of 10, SD = 1
x2 <- rnorm(100, 15, 1) #mean of 15, SD = 1
x1x2 <- x1*x2
x1c <- x1 - mean(x1)
x2c <- x2 - mean(x2)
x1x2c <- x1c * x2c
cr1[i] <- cor(x1c, x1x2c)
cr2[i] <- cor(x2c, x1x2c)
r1[i] <- cor(x1, x1x2)
r2[i] <- cor(x2, x1x2)
}
# r(x1,x2) should be zero because generated independently
res <- data.frame(r1, r2, cr1, cr2)
round(colMeans(res), 3)## r1 r2 cr1 cr2
## 0.829 0.551 -0.001 0.008On average, the correlations of the centered variables are 0 or near 0. They are not always zero and plotting the distribution shows the range of correlations.
library(dplyr)
library(tidyr)
library(ggplot2)
mm <- gather(res, key = 'vars', value = 'r')
mm %>% ggplot(aes(x = r)) +
geom_histogram(bins = 60) + facet_grid(~vars) +
theme_bw()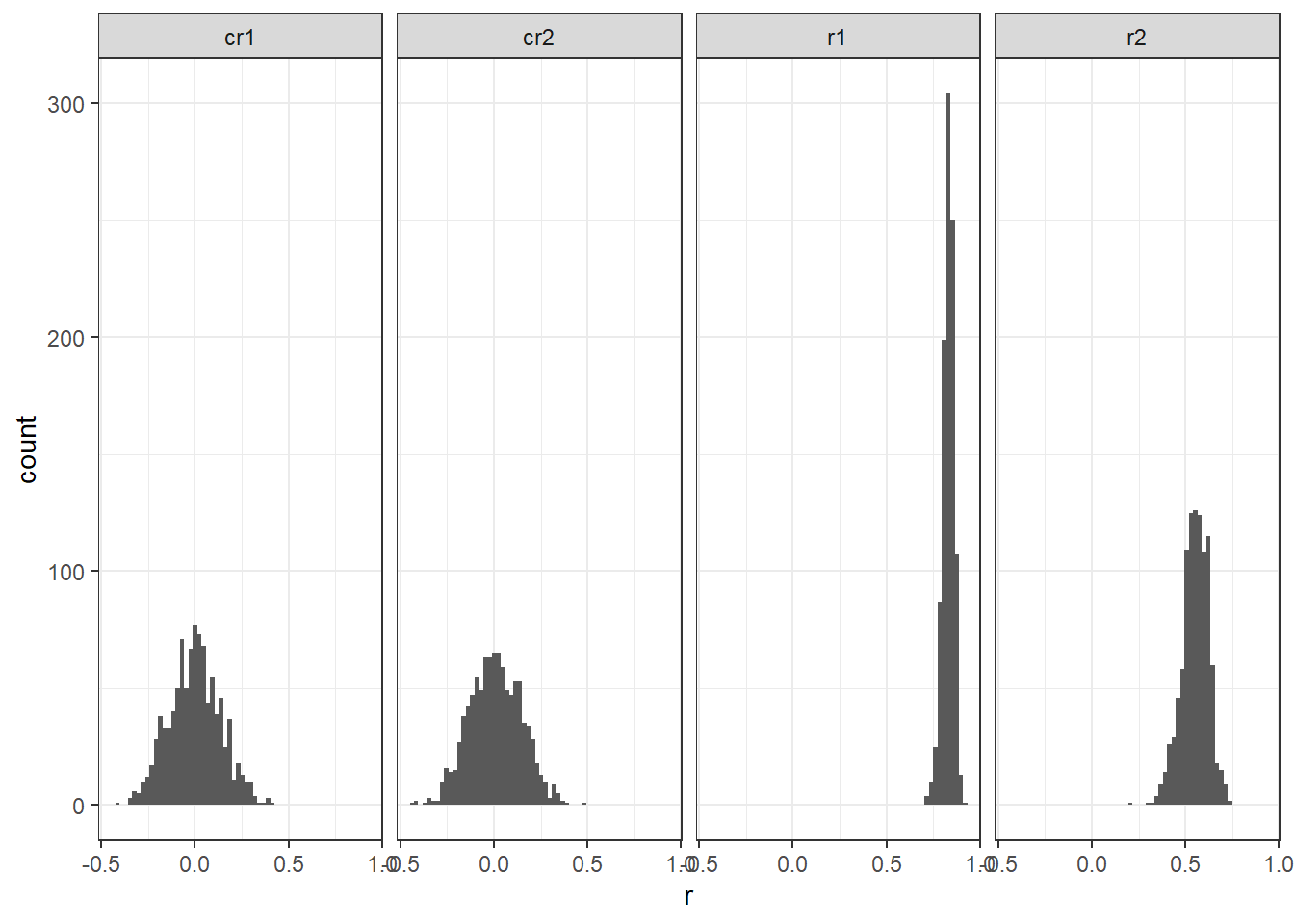
– END